5 Steps to Learn DSA from Scratch
Learn a programming language of your choice
Learn about Time and Space complexities
Learn the basics of individual Data Structures and Algorithms
Practice, Practice, and Practice more
Compete and Become a Pro
Introduction
DSA, or Data Structures and Algorithms, are fundamental concepts in computer science. Data structures are ways to organize and store data, while algorithms are step-by-step procedures for solving problems. Proficiency in DSA is crucial for developing efficient software and solving complex computational challenges.
1. Learn a programming language of your choice
Learning a programming language of your choice is crucial for cracking Data Structures and Algorithms (DSA) interviews. DSA is a fundamental concept in computer science, and it requires a solid understanding of programming languages to be successful. By mastering a programming language, you will not only be able to demonstrate your technical skills but also showcase your problem-solving abilities.
It is recommended to choose a language that you are comfortable with and that is widely used in the industry, such as Java, Python, or C++. Once you have chosen your preferred language, it is essential to practice coding exercises and solve DSA problems. There are various online resources and coding platforms available that provide a vast collection of DSA problems and offer different levels of difficulty. By practicing regularly and improving your programming skills, you will be better prepared for DSA interviews and increase your chances of landing a job in the tech industry.
2. Learn about Time and Space complexities
If you're preparing for a DSA (Data Structures and Algorithms) interview, it's important to have a solid understanding of time and space complexities. Time complexity refers to how much time an algorithm takes to execute as the input size grows, while space complexity refers to how much memory an algorithm uses as the input size grows.
Understanding these concepts is crucial because interviewers often ask questions that require you to analyze and optimize the time and space complexity of an algorithm. To prepare for these types of questions, you should practice analyzing the time and space complexities of common algorithms, such as sorting and searching algorithms, and be able to identify the best algorithm for a given problem based on its time and space complexity.

Additionally, you should be able to explain your thought process and reasoning behind your solution to demonstrate your understanding of these concepts. By mastering time and space complexities, you'll be better equipped to ace your DSA interviews and land the job of your dreams.
3.Data Structures and Algorithms
When it comes to cracking DSA (Data Structures and Algorithms) interviews, it's important to have a strong understanding of the fundamentals. Data structures like arrays, linked lists, stacks, queues, trees, and graphs are essential building blocks for solving complex algorithmic problems.
Understanding the time and space complexity of different operations on these data structures is crucial for optimizing your solutions. Algorithms like sorting, searching, dynamic programming, and graph algorithms are also important to master. It's important to know the different approaches for solving a problem and to be able to choose the most efficient one. In addition to technical knowledge, it's also important to practice problem-solving skills.
3.1 Arrays & Strings
The first topic that we start with within the Data Structures roadmap is Arrays. An array is a collection of homogeneous elements stored in a contiguous block of memory. The size of an array is always pre-defined. For a visual representation, take a look at the following diagram.
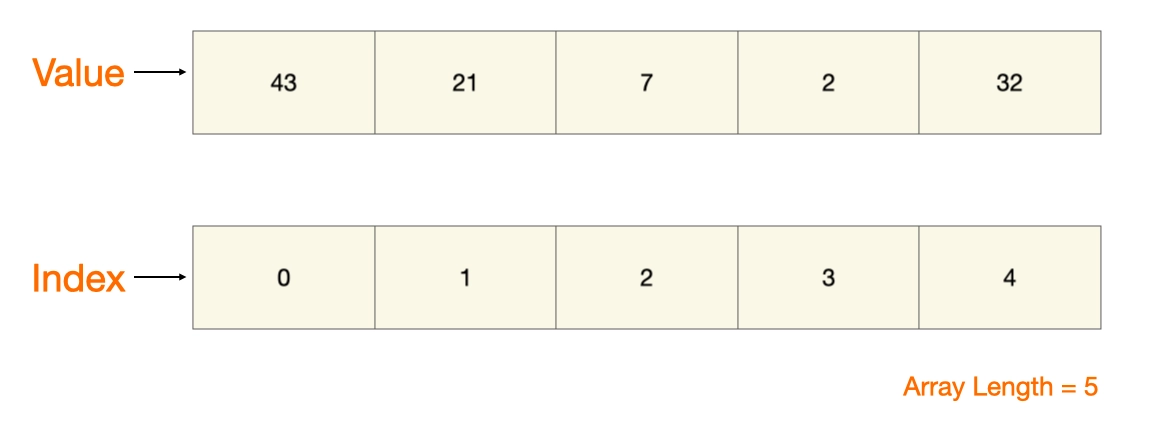
Every element (denoted as 'Value') has a corresponding index number. For example, for an array of length 5, the index numbers increment as 0, 1, 2, 3, and 4. An array that consists of characters as elements is called a string. What makes it different from a character array is that it ends with a special symbol ' \0'.
Some essential sub-topics from Arrays and Strings that are important for placements are given below. In addition, every topic is linked to its Coding Ninjas Studio page for you to understand and practice.
Basic Array And Strings Questions
Kadane's Algorithm
Dutch National Flag Algorithm
3.2 Multidimensional Arrays
Arrays can be one-dimensional or multi-dimensional. Multi-dimensional array concepts are applied at very important places like in matrices. A visual representation would be such:
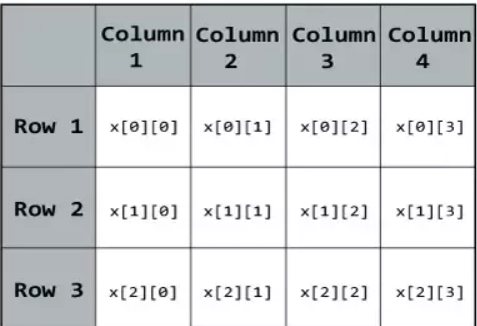
The most important problems from this topic are Traversal Based Problems and Rotation based problems.
Searching and Sorting

Searching
Searching means to find out whether a particular element is present in the given array/list. For instance, when you visit a simple google page and type anything that you want to know/ask about, basically you are searching that topic in Google's huge database for which google is using some technique in order to provide the desired result to you.
There are basically two types of searching techniques:
Linear search
Binary search
Linear Search
It is a simple sequential search over all the elements of the array, and each element is checked for a match, if a match is found return the element otherwise the search continues until we reach the end of the array.
Pseudocode:
/*
array from leftidx(0) to rightidx(arr.length-1) is considered
*/
function linearSearch(arr, leftidx , rightidx , target)
// Search for the target from the beginning of arr
for idx = 0 to arr.length-1
if arr[idx] == target
return idx
// target is not found
return -1
Time complexity: O(N), as we traverse the array only once to check for a match for the target element.
Space complexity: O(1), as no extra space is required.
Binary Search
Search in a sorted array by repeatedly dividing the array into two halves and searching in one of the halves.
Suppose you want to find a particular element in the sorted array, then following this technique, you have to traverse all the array elements for searching one element but guess if you only have to search at most half of the array indices for performing the same operation. This can be achieved through binary search.
Now, let's look at what binary searching is.
Let us consider the array:
0 1 2 3 4
1 2 3 4 5
Given an array of size 5 with elements inside the boxes and indices above them. Our target element is 2.
Steps:
Find the middle index of the array.
Now, we will compare the middle element with the target element. In case they are equal then we will simply return the middle index.
In case they are not equal, then we will check if the target element is less than or greater than the middle element.
In case, the target element is less than the middle element, it means that the target element, if present in the given array, will be on the left side of the middle element as the array is sorted.
Otherwise, the target element will be on the right side of the middle element.
- This helps us discard half of the length of the array each time and we reduce our search space to half of the current search space.
In the example above, the middle element is 3 at index 2, and the target element is 2 which is greater than the middle element, so we will move towards the left part. Now marking start = 0, and end = n/2-1 = 1, now middle = (start + end)/2 = 0. Now comparing the 0-th index element with 2, we find that 2 > 1, hence we will be moving towards the right. Updating the start = 1 and end = 1, middle becomes 1, comparing the 1-st index of the array with the target element, we find they are equal, meaning from here we will simply return 1 (the index of the element).
Advantages of Binary search:
This searching technique is fast and easier to implement.
Requires no extra space.
Reduces time complexity of the program to a greater extent i.e O(logN), where N is the number of the elements in the array, provided the given array is already sorted.
Pseudocode:
/*
array of size N from 0 to N-1 is considered
*/
function binarySearch(arr, N, target)
// Initializing lo and hi pointers
lo = 0
hi = N-1
// Searching for the target element until lo<=hi
while lo <= hi
// Finding the mid of search space from lo to hi
mid = lo + (hi-lo)/2
// If the target element is present at mid
if arr[mid] == target
return mid
/*
If the target element is less than arr[mid], then if the target is
present, it must be in the left half.
*/
if target < arr[mid]
hi = mid-1
// Otherwise if the target is present, it must be in the right half
else
lo = mid+1
// If the target is not found return -1
return -1
Time complexity: O(logN), where N is the number of elements in the array, given the array is sorted. Since we search for the target element is one of the halves every time, reducing our search space to half of the current search space.
Since we go on searching for the target until our search space reduces to 1, so
Iteration 1- Initial search space: N
Iteration 2 - Search space: N/2
Iteration 3 - Search space: N/4
Let after ‘k’ iterations search space reduces to 1
So, N/(2k) = 1
\=> N = 2k
Taking Log2 on both sides:
\=> k = log2N
Hence, the maximum number of iterations ‘k’ comes out to be log2N.
Space complexity: O(1), as no extra space is required.
Sorting
Sorting means an arrangement of elements in an ordered sequence either in increasing(ascending) order or decreasing(descending) order. Sorting is very important and many software and programs use this. The major difference is the amount of space and time they consume while being performed in the program.
For a detailed explanation of types of sorting algorithms that are generally used, please refer to the topic Sorting Algorithms.
3.3 Recursion and Backtracking
Recursion is a programming technique in which a function calls itself, directly or indirectly. It is majorly used in complex problems where we can divide the main problem into smaller subproblems.
![]()
Backtracking is a programming technique that uses recursion to build an overall solution by incrementally going through smaller levels of the problem until the solution is reached.
The topics under this category that you must master are given as follows.
Basic Recursion Questions
Divide And Conquer
Popular Problems
Mixed Problems
3.4 Sorting Algorithms
When we have such astronomical amounts of data, doing operations on it requires it to be ordered in a particular manner depending on the final usage. There are various types of sorting algorithms that are used to sort data. These are important from the perspective of studying for interviews.
Continuing the data structures roadmap, the two most important sorting algorithms are Insertion Sort and Selection Sort.
3.5 Binary Search Applications
The next topic in the data structures roadmap is Binary Search. Binary Search is a searching algorithm that works on the principle of divide and conquer. It works by comparing the target element to the middle element of the collection. A new collection is formed after every comparison by repeatedly dividing the main collection into halves. Important problems to practice from this topic are:
Binary Search on Arrays
Binary Search on Matrices
Mixed Problems
3.6 Linked Lists
Linked List is a dynamic linear data structure that consists of nodes where each node consists of two fields – data and pointer. First, take a look at the visual representation of Linked Lists:
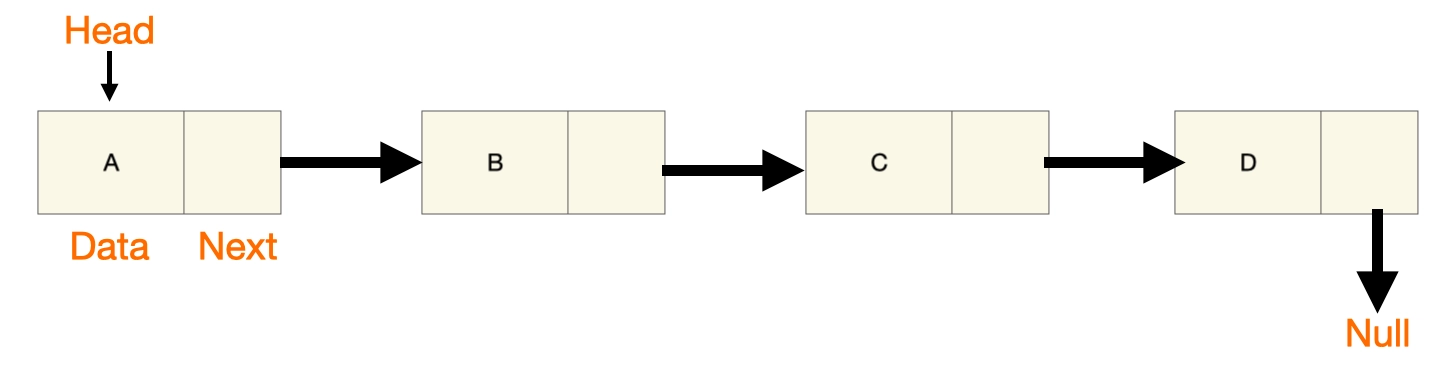
The first node is called the Head and consists of a pointer that points to the second node. Similarly the second node points to the third node and so on. Linked Lists are of three types - Singly Linked List, Doubly Linked List and Circular Linked List.
Some important problems from this topic are as follows:
Reversal Problems
Sorting Problems
Slow And Fast Pointers
Modify In Linked list
3.7 Stacks and Queues
Stack and Queue, both are linear data structures. Stacks work on the principle of LIFO (Last In First Out), whereas Queues work on LILO (Last In Last Out). A visual representation of both would make things clearer.
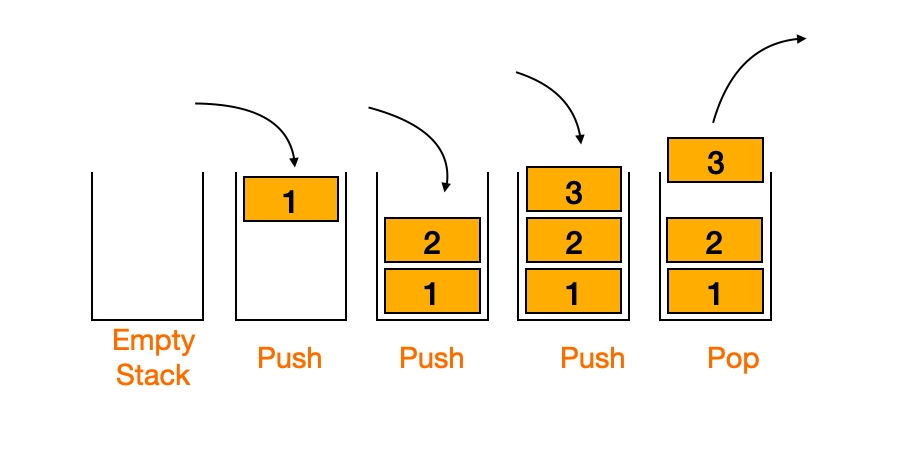
Above is a representation of a stack. Inserting an element into a stack is termed 'Pushing', and deletion of an element from the stack is termed 'Popping'.
Now let’s see how Queues look.
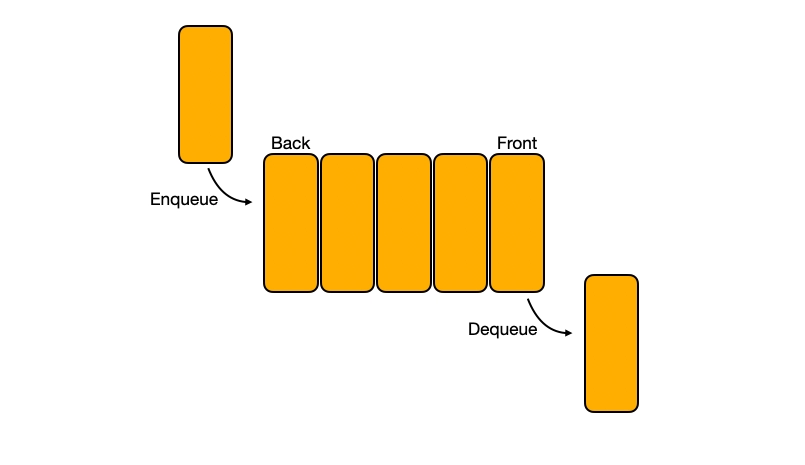
You can see from the above diagram that, a Queue has a Front and a Back. Addition of an element to the queue is done to the Back and deletion of an element from the queue is done from the Front. The former is termed as ‘Enqueuing an element’ and the latter as ‘Dequeuing an element’.
There are two sets of problems under these two topics that are important to be mastered - Implementation Based Problems and Application Based Problems. Head to the links to start practicing.
3.8 Binary Trees
The next step in the data structures roadmap is the Binary Tree. A Binary tree is a type of tree data structure in which every node has at most two children. Each node consists of three fields – data, a pointer to the left child, and a pointer to the right child. Some important concepts to master from this topic are given below.
Construction Of BST
Conversion Based Problems
Modification in BST
Standard Problems
3.9 Priority Queues and Heaps
A priority queue is a queue in which every value is associated with a priority. Dequeuing takes place in a manner that the element with a higher priority is dequeued before an element with a lower priority. Heaps are a special type of data structure which are based on complete binary trees.
There are three kinds of problems part of the data structures roadmap that are important to be mastered from this topic:
Implementation Based problems
Conversion based problems
K Based Problems
3.10 Graphs
A Graph is a non-linear data structure that consists of nodes and edges. A node is a vertex and an edge is a line or curve that connects any two vertices. Some important concepts to be mastered in this topic are given below.
Graph Traversals - BFS And DFS
DFS Algorithm
MST
Shortest Path Algorithms
Topological Sort
Graphs in Matrix
3.11 Dynamic Programming
A very important topic in the data structures roadmap is Dynamic Programming. It is an optimization technique working on recursion in which we divide a complex problem into smaller subproblems. It finds many applications in computer science. Some important concepts from this topic are given below.
DP with Arrays
DP With Strings
DP With Maths
DP With Trees
Breaking And Partition Based Problems
Counting Based Problems
4. Practice, Practice, and Practice more
The key to getting better at any skill is practicing. You should make practicing DSA questions a part of your routine during your preparation. Most DSA websites have a problem-of-the-day feature that can help you maintain your consistency, and has this feature as well.
![]()
5. Compete and Become A Pro
Competing in contests is the most important part of getting better at DSA. When it comes to solving questions in online assessments, time is the most important aspect. Time is the most important aspect of performing well in online assessments. You should regularly participate in coding contests on various platforms to improve your problem-solving speed.
Conclusion
In this article, we discussed the importance of Data structures and then laid down a data structures roadmap going topic-wise and listing down the most important concepts from each topic. Mastering these concepts will give a boost to your preparation for interviews in which data structures are one of the most important topics.
